토픽모형과 Sampling-Based Estimation
(표집-근거 추정)

김성현 (Fuller Graduate School of Psychology)

본 글은 Latent Dirichlet Allocation (LDA; 잠재디리클레할당; Blei, Ng, & Jordan, 2003)와 같은 토픽모형 등을 비롯한 베이지언 모형 추정에서 자주 사용하는 표집-근거 추정에 대해 서술하고자 한다.

LDA와 같은 토픽모형의 주 목적은 단어-문서-글뭉치 순으로 위계적으로 구성된 텍스트 자료에서 (1) 토픽 (단어들의 확률분포), (2) (각 문서 내의) 토픽 분포, 그리고 (3) (각 단어의 특정) 토픽(에로의) 할당 등의 3 가지 잠재변수를 추정하는 것이라 할 수 있다. 이 모형에서 관찰변수는 (observed variable) 텍스트 자료이고, 이렇게 텍스트 자료만을 활용하여 여러 잠재변수를 추정하는 데는 상당한 애로가 따를 수밖에 없다. 이러한 어려움을 극복하기 위해서 크게 두가지 ‘근사’ (approximation) 추정 방법을 사용하는데 첫번째 방법은 표집-근거 추정인데 가장 많이 사용하는 방법은 Gibbs sampling (깁스 표집)이다. 두번째 방법은 최적화 (optimization) 기법에 기초한 Variational Inference이다. 본 글은 그 중 첫번째 방법에 대해 설명하고자 한다.

표집-근거 추정법은 Monte Carlo method라고도 하는데 목표로 하는 값의 정확한 추정이 어려울 때 사용하는 방법이다. 예를 들어, 원주율(π)의 정확한 값을 구하고자 할 때 특정 수식을 풀어서 구할 수 없기 때문에 이를 근사적으로 구하는 방법 밖에 없다. 그 한 예로 아르키메데스의 내접/외접 다각형을 활용한 방법이 있다. 또 다른 방법으로 표집-근거 추정 방법을 활용할 수 있다.

아래 그림은 한 변의 길이가 2인 정사각형에 내접한 지름이 2인 원을 나타낸 것이다. 정사각형의 면적은 2×2=4이고 원의 면적은 π×12=π가 될 것이다. 만약 무작위로 수 많은 점을 (각 점이 하나의 표집 (sample)) 정사각형 안에 균등하게 (어느 한 쪽에 치우치지 않고) 찍는다면 π/4의 비율로 원안에 점이 찍힐 것이다. 이럴 때, 정사각형 안에 찍힌 전체의 점 중 몇 개가 원 안에 있는지 세어 보면 π의 근사값을 계산할 수 있다. 원 안에 있는 점의 개수가 n이라고 할 때 π = 4×n이 된다. R 프로그램 언어로 (R Core Team, 2018) 작성한 프로그램을 부록으로 첨부한다.

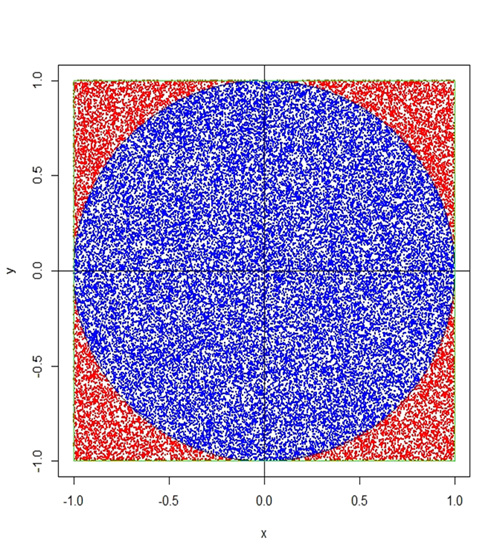
토픽모형, 특히 LDA에서 사용하는 깁스 표집 방법은 위의 π를 구하는 방법과 표집-근거 추정라는 점에서 동일하지만 좀 더 복잡하다. 주요한 차이점은 π를 구하는 방법에서는 표집들이 상호 독립이지만 (0 상관), 깁스 표집 방법에서는 조건분포를 사용하여 표집하기 때문에 표집의 순서가 가까울수록 상관이 높다는 것이다. 이러한 단점을 보완하기 위해서 깁스 표집에서는 특정 순서의 표집만을 (매 10회째 표집) 추정에 사용하거나 표집 초기에 (burn-in 혹은 warm-up period) 생성된 표집을 버리고 안정기 이후의 표집만을 사용하기도 한다.

LDA 모형에서 사용하는 깁스 표집 방법 중의 하나는 Collapsed Gibbs sampling인데 (CGS), 이 방법에서는 LDA의 3가지 잠재변인을 동시에 추정하지 않고 먼저 토픽 할당만을 깁스 표집으로 추정한 다음 그 결과를 활용하여 나머지 두 잠재변인을 추정한다. 구체적으로 토픽할당 (보통 ‘z’라고 표시)을 CGS 방법으로 추정할 때, p(zi = j | z-i, w, α, β) 와 같은 조건부 확률을 계산하여 각 단어의 각 토픽에 할당될 확률을 계산하고 그 결과를 바탕으로 각 단어는 가장 확률이 높은 토픽에 할당된다. 앞의 조건부 확률 공식에서 p(∙)는 확률이라는 의미이고 zi는 i번째 단어에 할당된 토픽을 나타낸다. j는 특정 토픽이며 그리고, z-i는 i번째 단어를 제외한 모든 단어들에 할당된 토픽이고 w는 모든 단어들을 나타낸다. 그리고, α, β는 LDA 모형의 다른 모수들로 연구자가 지정하는 값이다.