토픽모형과 디리클레(Dirichlet) 분포

김성현(Fuller Graduate School of Psychology)

Dirichlet 분포는 Latent Dirichlet Allocation (LDA; 잠재디리클레할당; Blei, Ng, & Jordan, 2003)라는 모형의 이름을 보면 알 수 있듯이 LDA와 같은 토픽모형의 기본을 이루는 분포이다. 그래서 토픽모형을 정확하게 그리고 깊게 이해하기 위해서는 Dirichlet 분포를 제대로 이해하는 것이 필수적이다.

Dirichlet 분포의 가장 중요한 특징은 다항분포와 (multinomial distribution) 쌍을 이루는 켤레분포라는 (conjugate distribution) 점이다. LDA와 같은 베이지언 통계 모형에서는 연구자의 주관이 개입되는 사전분포와 연구자료에서 파악한 우도 (likelihood)를 결합하여 사후분포를 구하여 모수를 추정한다. 구체적으로 LDA 모형에서는 Dirichlet 분포가 사전분포의 역할을 하고 다항분포는 우도의 역할을 담당하며 사전분포와 우도를 곱하여 얻게 되는 사후분포는 켤레분포의 특성 때문에 다시 Dirichlet 분포가 된다.

LDA에서 Dirichlet 분포와 다항분포는 서로 역할을 분담하는데 전자는 글뭉치 전체를 포괄하는 상위의 분포를 설명하고 후자는 텍스트 자료 내의 하위 분포를 직접 설명하는 역할을 담당한다고 할 수 있다. 앞서 다른 웹진에서 LDA와 같은 토픽모형의 주 목적은 단어-문서-글뭉치 순으로 위계적으로 구성된 텍스트 자료에서 (1) 토픽 (단어들의 확률분포), (2) (각 문서 내의) 토픽 분포, 그리고 (3) (각 단어의 특정) 토픽(에로의) 할당 등의 3 가지 잠재변수를 추정하는 것이라 할 수 있다고 말한 바 있다. 예를 들어, 1과 2의 토픽과 토픽분포 등과 관련지어 설명하자면, 전체 글뭉치 내의 모든 토픽들의 분포는 Dirichlet 분포를 따르지만 개별 토픽 내에서 단어들의 분포는 다항분포를 따르는 것으로 LDA는 가정한다. 마찬가지로, 전체 문서들 내의 토픽 분포는 Dirichlet 분포를 따르지만 개별 문서 내의 토픽분포는 다항분포를 따르는 것으로 LDA는 가정한다. 마지막으로 3번의 토픽할당은 각 문서 내의 각 단어에 (구체적 텍스트 자료) 해당되며 하위 요소에 해당하기 때문에 다항분포를 따르는 것으로 LDA는 가정한다.

앞서 Dirichlet 분포는 LDA 모형에서 사전분포 역할을 하며 베이지언 통계에서 사전분포에는 연구자의 주관이 개입될 수 있다. 그러면 어떻게 연구자의 주관이 LDA 모형에 개입될 수 있는 것인가? Dirichlet 분포의 패러미터는 α인데 (Dir(α)) 로 표현) 항상 0보다 큰 양의 수이고 정규분포의 패러미터가 평균과 표준편차의 둘인 것처럼 Dirichlet 분포에서는 패러미터가 α 하나이다. 단, Dirichlet 분포는 3개 이상의 차원을 가진 다변인 분포여서 α는 벡터이고 벡터의 길이가 차원이 된다. 예를 들어, 3차원 Dirichlet 분포는 Dir(α1, α2, α3)로 표현한다. LDA에서는 개별 α값이 동일한 대칭 Dirichlet 분포를 사용한다 (예: α1 = α2 = α3).

그림 1의 정삼각형의 도표는 3차원의 Dirichlet 분포를 나타낸 것인데 simplex 도표라고도 하며, 그림 1은 simplex 도표의 해석을 돕기 위해 만든 것이다. 이 그림에는 3개의 토픽으로 (3차원) 구성된 LDA 모형에서 도출한 4개의 문서가 4개의 파란색 다각형으로 표시되어 있다. 먼저 각 토픽은 simplex 도표에서 하나의 축을 이루고 그 범위는 0부터 1이다. 각 토픽의 꼭지점은 1 (100%)의 값을 나타내고 반대편 밑변의 값은 0을 나타낸다. 각 파란색 다각형은 3개 토픽의 비율로 나타낼 수 있는데 예를 들어, 정사각형 문서는 토픽 1부터 토픽 3까지 그 비율이 (.6, .2, .2)이고 토픽 1이 60%, 토픽 2와 3이 각각 20%를 차지하는 문서이다 (합계 100%). 마찬가지로 정삼각형 문서는 토픽 비율이 (.4, .1, .5)이고 마름모 문서는 (.2, .2, .6), 원 문서는 (.2, .4, .4)이다.

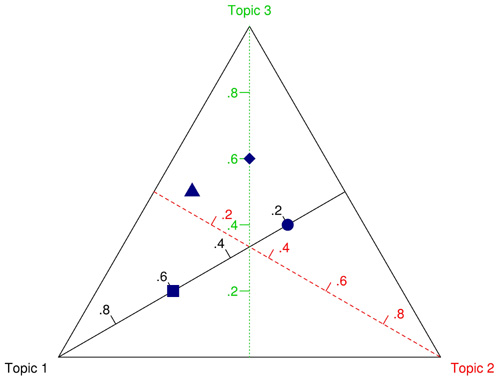
그림 1. 4개의 문서와 3개의 토픽으로 구성된 3차원의 simplex 도표.

α는 concentration 패러미터라고 하는데 LDA에서 α값을 1보다 크게 설정하면 각 문서 내의 토픽분포가 균질해지는 반면 (해당 문서에서 특정 토픽이 독점할 확률이 작아지고) 만약 α값을 1보다 작게 설정하면 각 문서 내의 토픽분포가 불균질해지고 특정 토픽이 각 문서를 독점할 확률이 높아지게 된다. 아래 정삼각형의 도표들은 3차원의 Dirichlet 분포들을 나타낸 것이다. 각 도표에는 (이러한 도표를 simplex 도표라고 한다) Dirichlet 분포에서 무작위로 표집한 1000개의 점들이 있는데 각 점은 각각 하나의 다항분포를 나타낸다.

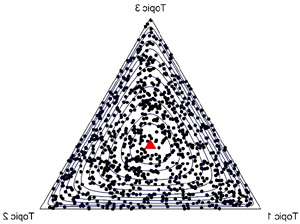
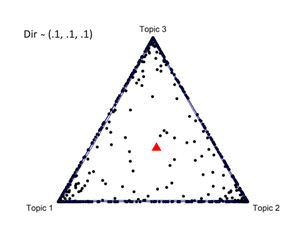
그림 2-5는 3차원의 Dirichlet 분포를 나타낸 것인데 그림 2-4는 대칭 Dirichlet이지만 그림 5는 비대칭 Dirichlet 분포이다. 각 그림 중간의 빨간 삼각형은 각 Dirichlet 분포의 평균값이고 대칭분포의 경우 평균값은 (1/3, 1/3, 1/3)로 동일하다. 그림 2-4를 잘 살펴보면Dirichlet 분포에서 왜 α를 concentration parameter라 부르는지 단서를 알 수 있다. 그림 3의 경우, (α = 100) 토픽분포가 균질하지만, 그림 4는 특정 토픽의 독점도가 심하다. 그림 2의 경우 (α = 1)로서 그림 3과 4의 중간 특징을 보여준다.

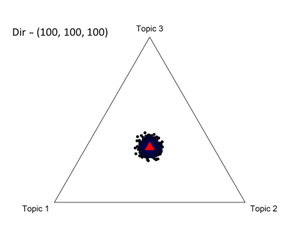그림 2. Dir(1, 1, 1)	그림 3. Dir(100, 100, 100)
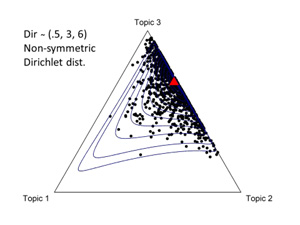그림 4. Dir(.1, .1, .1)	그림 5. Dir(.5, 3, 6)

이러한 α의 특성은 LDA 분석에 있어 연구자의 주관적 개입의 통로로 활용될 수 있는데, 연구자는 현재 분석대상 텍스트 자료들이 여러 토픽들을 균질하게 배합한다고 생각하면 α 값을 1보다 크게 하여 LDA 모형을 추정하는 반면 각 문서를 1-2개의 소수 특정 토픽이 독점한다고 생각하면 α 값을 1보다 작게 할 필요가 있다. 마찬가지로 LDA 모형에서 역시 Dirichlet 분포에서 나온다고 가정하는 토픽 (β concentration parameter)에도 동일한 내용을 적용할 수 있다.

부록으로 무작위로 Dirichlet 분포를 생성하는 R code를 싣는다. R 프로그램에는 이러한 프로그램이 실려있지 않아서 연구자가 각자 만들어서 사용해야 한다. 이 코드는 Dirichlet 분포 이해에 도움을 줄 것이다.